| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 완전탐색
- 프로그래머스
- Matplotlib
- wandb
- leetcode
- pytorch
- 네이버AItech
- 코딩테스트
- rnn
- vscode
- autoencoder
- GIT
- 알고리즘
- FDS
- pep8
- GCP
- DeepLearning
- 백준
- github
- torchserve
- datascience
- Kubernetes
- FastAPI
- python
- NLP
- GitHub Action
- Kaggle
- PytorchLightning
- NaverAItech
- docker
- Today
- Total
Sangmun
[NLP] Seq2Seq 본문
논문링크
https://arxiv.org/abs/1409.3215
Sequence to Sequence Learning with Neural Networks
Deep Neural Networks (DNNs) are powerful models that have achieved excellent performance on difficult learning tasks. Although DNNs work well whenever large labeled training sets are available, they cannot be used to map sequences to sequences. In this pap
arxiv.org
개요
Sequence to Sequence는 2014년에 발표된 논문으로 LSTM 구조를 활용한 기계번역에 사용된 방법론이다. 기존의 확률을 기반으로 한 기계번역 보다 월등한 성능을 보여주어서 2017년에 Transformer가 나오기 전까지는 State-of-the-art 였던 방법론이다.
참고자료
https://docs.chainer.org/en/v7.8.0/examples/seq2seq.html
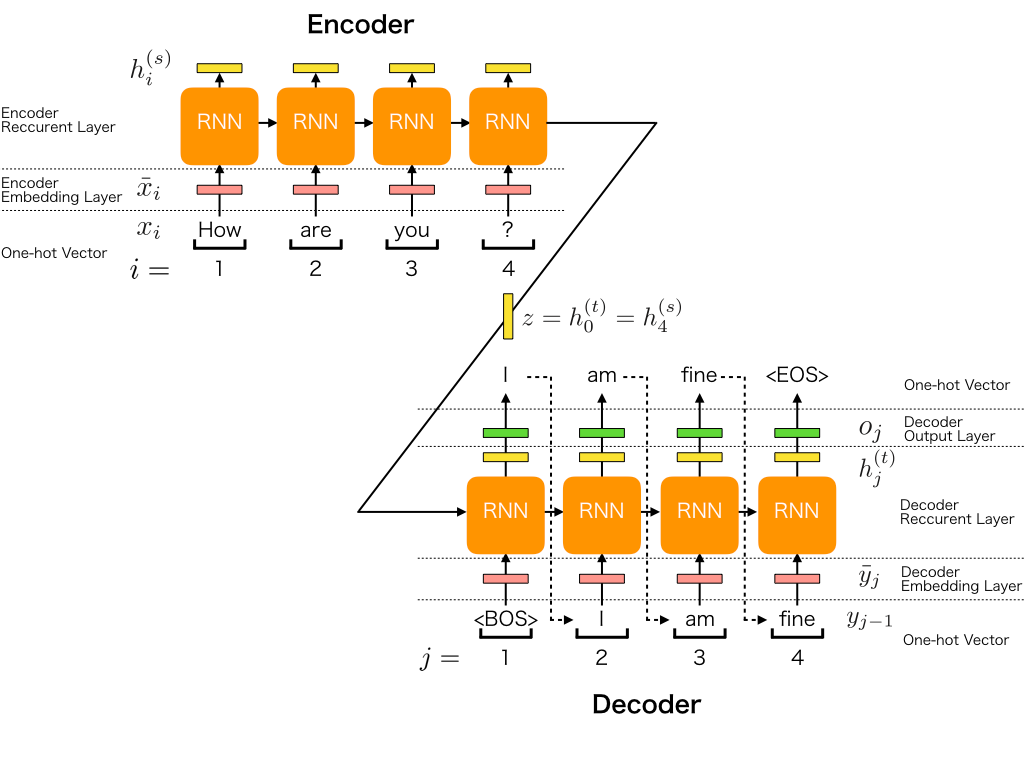
아래와 같은 데이터 세트가 있음을 가정하면(x^i는 src 언어, y^i는 dest언어)
$$ D = \begin{Bmatrix} x^i,y^i \end{Bmatrix}_{i=1}^{N} $$
$$ x^i = \begin{Bmatrix}x^i_1,\cdots,x^i_m \end{Bmatrix} \; and \; y^i = \begin{Bmatrix}y^i_0,y^i_1,\cdots,y^i_n \end {Bmatrix}, $$
$$ where \; y_0 = and <BOS> and \; y_n = <EOS> $$
우리의 목적은 아래와 같은 함수의 값을 최대화시키는 세타햇 값을 찾는 것이며
$$ \hat {\theta} = \underset {\theta\in\Theta}{argmax}\sum_{i=1}^{N} logP\begin {pmatrix} y^i|x^i;\theta\end {pmatrix} $$
$$ = \underset {\theta\in\Theta}{argmax}\sum_{i=1}^{N}\sum_{j=1}^{n} logP\begin {pmatrix} y^i|x^i, y^i_{<j};\theta\end {pmatrix} $$
아래와 같은 Loss function의 gradient descent로 우리가 원하는 세타값을 찾아 번역의 성능을 높일 수가 있다.
$$ \mathcal{L}(\theta)= -\sum_{i=1}^{N}\sum_{j=1}^{n}logP\begin{pmatrix}y^i|x^i,y^i_{<j};\theta\end{pmatrix} $$
$$ \theta \leftarrow \theta - \alpha\bigtriangledown_\theta \mathcal{L}(\theta) $$
Encoder의 구조

한 개 타입스텝의 encoder의 hidden_state는 아래와 같이 계산되며 ( |V_s|는 src 언어의 단어집합의 크기)
$$ h^{enc}_t = RNN_{enc}(emb_{enc}(x_t),h^{enc}_{t-1}), \; where \; h^{enc}_{0} = 0. $$
$$ |x^i| = (bs,m,|v_s|) \; |x^i_t| = (bs,1,|v_s|) $$
최종적으로 모든 RNN 셀에서 나온 hidden_state들은 아래와 같다(여기서 m = 4)
$$ h^{enc}_{1:m} = [h^{enc}_1;\cdots;h^{enc}_m], $$
$$ |h^{enc}_{1:m}| = (bs, m, hs) $$
$$ where \; h^{enc}_t \in \mathbb{R}^{batch\_size \times 1 \times hidden\_size} \; and \; h^{enc}_{1:m} \in\mathbb{R}^{batch\_size \times m \times hidden\_size}. $$
만약 RNN이 bidirectional한 구조라면 hidden_state들의 출력의 크기는 아래와 같다.
$$ h^{enc}_t \in \mathbb{R}^{batch\_size \times 1 \times (2 \times hidden\_size)} \; and \; h^{enc}_{1:m} \in \mathbb{R}^{batch\_size \times m \times (2 \times hiddens\_size)}. $$
Decoder의 구조

한개 타입스텝의 decoder의 hidden_state는 아래와 같이 계산되며 (|V_t|는 target언어의 단어집합의 크기, 여기서 m=4)
$$ h^{dec}_t = RNN_{dec}(emb_{dec}(\hat{y}_{t-1}),h^{dec}_{t-1}), \; where \; h^{dec}_0 = h^{enc}_m. $$
$$ |y^i| = (bs,n,|v_t|) \; |y^i_t| = (bs,1,|v_t|) $$
decoder cell들에서 나온 출력값의 사이즈들은 아래와 같다.
$$ h^{dec}_{1:n} = [h^{dec}_1;\cdots;h^{dec}_n] $$
$$ |h^{dec}_{1:m}| = (bs,n,hs) $$
auto regressive 한 성질을 가졌음으로 uni direction만 사용한다.
Generator의 구조

decoder cell을 거쳐 나온 값을 다시 Linear layer(W_gen)를 거쳐 1*hidden_size로 나온 벡터 값을 다시 |V_t|사이즈로 바꿔주며 최종적으로 softmax layer를 거쳐 하나의 단어를 예측을 하게 된다.
$$ \hat{y}_t = softmax(h^{dec}_t \cdot W_{gen}), $$
$$ where \; h^{dec}_t \in \mathbb{R}^{batch\_size \times 1 \times hidden\_size} \; and \; W_{gen} \; \mathbb{R}^{batch\_size \times |V|}. $$
결론
LSTM구조를 활용하여 기존의 SMT 기반의 기계번역의 성능을 뛰어넘는 모델을 만들었으며 본 논문에는 언급되지 않았지만 몇가지 한계점이 존재하였다. 첫째는 하나의 고정된 크기의 벡터에 모든 정보를 압축을 시도함으로 정보 손실이 발생된다는 것이였고 두번째는 RNN 구조의 문제인 기울기 소실 문제가 발생한다는 것이였다.
이를 위한 대한으로 Attention 기법이 등장하게 되었다.
'네이버 AI 부스트캠프 4기' 카테고리의 다른 글
| [NLP] Beam Search (1) | 2022.10.15 |
|---|---|
| [NLP] Perplexity(PPL) and BLEU score (0) | 2022.10.14 |
| [NLP] Transformer (0) | 2022.10.03 |
| Pytorch Custom Dataset (2) | 2022.09.30 |
| 구글 colab vscode에서 접속하기(ngrok) (0) | 2022.09.29 |




