Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- vscode
- docker
- torchserve
- leetcode
- github
- 백준
- Kaggle
- GIT
- autoencoder
- FDS
- NLP
- python
- 네이버AItech
- PytorchLightning
- pep8
- 완전탐색
- 프로그래머스
- NaverAItech
- 알고리즘
- rnn
- wandb
- pytorch
- DeepLearning
- FastAPI
- Kubernetes
- GitHub Action
- GCP
- datascience
- 코딩테스트
- Matplotlib
Archives
- Today
- Total
Sangmun
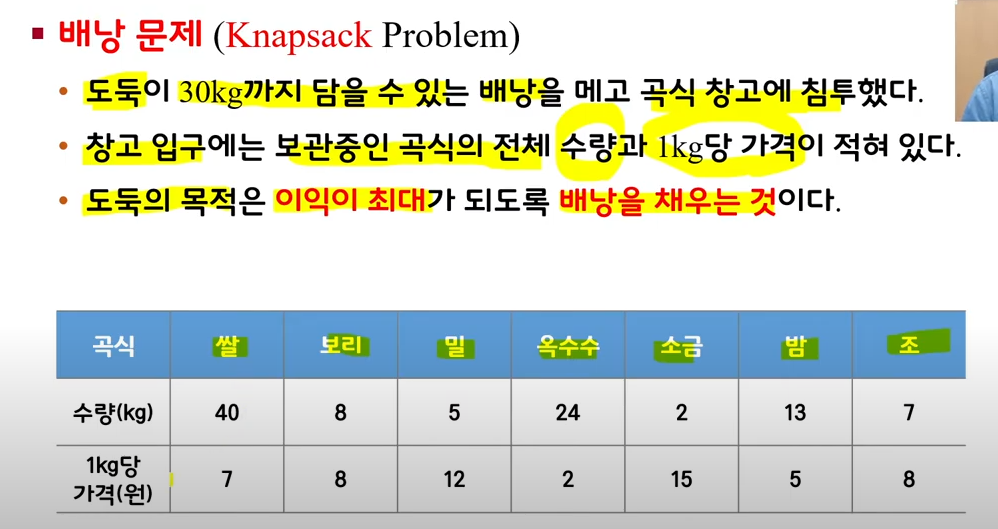
배낭 문제(냅색 문제) - 1 (분할가능한 배낭 문제) 본문
https://namu.wiki/w/%EB%B0%B0%EB%82%AD%20%EB%AC%B8%EC%A0%9C
배낭 문제 - 나무위키
무게 대비 가치가 다른 물건들을 일정한 용량의 용기에 담아야 한다는 기본 틀에서, 바리에이션이 많다. 가방이 여러 개인 문제, 고려할 변수가 무게와 가치 외에도 더 있는 3개 이상의 변수 문
namu.wiki
https://www.youtube.com/watch?v=8UVDnahV1eg
분할 가능한 배낭 채우기 문제
그리디 알고리즘으로 정렬을 해서 무게를 채워주면 된다.
Frational Knapsack Problem
탐욕알고리즘을 이용해서 최적의 해를 구할 수 있다.
def knapsack1(W,w,p):
n = len(w) - 1
K = [0] * (n + 1)
weight = 0
for i in range(1, n+1):
weight += w[i]
K[i] = w[i]
if (weight > W):
K[i] -= (weight - W)
break
return K
# 지금은 무게와 가치가 가치순으로 내림차순 정렬되어 있지만
# 보통은 안그럴 경우가 더 많다.
w = [0,2,5,8,7,40,13,24]
p = [0,15,12,8,8,7,5,2]
W = 30
K = knapsack1(W, w, p)
print(K, sum(K))
price = 0
for i in range(1, len(K)):
price += p[i] * K[i]
print("Total price is", price)
탐욕 알고리즘은 최적해를 보장하는가?
* 아이템의 분할이 가능하면 Greedy가 최적해를 찾아줌
* 하지만 분할이 가능하지 않다면 -> 최적해가 아닐 가능성이 더 높음
'알고리즘 > 알고리즘(초급)' 카테고리의 다른 글
| 배낭 문제(냅색 문제) - 2(분할 불가능한 냅색 문제) (0) | 2022.12.20 |
|---|---|
| python queue 구현 (0) | 2022.12.04 |
| python 으로 stack 직접 구현하기 (0) | 2022.12.04 |
| 투포인터 (0) | 2022.11.23 |
| 백트래킹을 이용한 부분 집합을 구하는 알고리즘 (0) | 2022.11.21 |
Comments
